Unveiling the Unseen: Peeking into a Four-Dimensional Realm

A Curious Look Beyond Our Familiar Three-Dimensional World

Ever pondered a world unbound by the usual length, width, and height? Picture this: movement isn’t just forward, backward, left, right, or up and down, but in a completely new, right-angled direction. This is the concept of four spatial dimensions, a notion that sparks the imagination of mathematicians, physicists, and anyone with a curious mind. While we, as beings accustomed to three dimensions, can’t directly experience this higher-dimensional space, thinking about its theoretical possibilities offers a fascinating peek into the potential intricacies and marvels of the universe. It’s a bit like trying to describe a square to someone who’s only ever known a line — it demands a bit of a mental stretch.

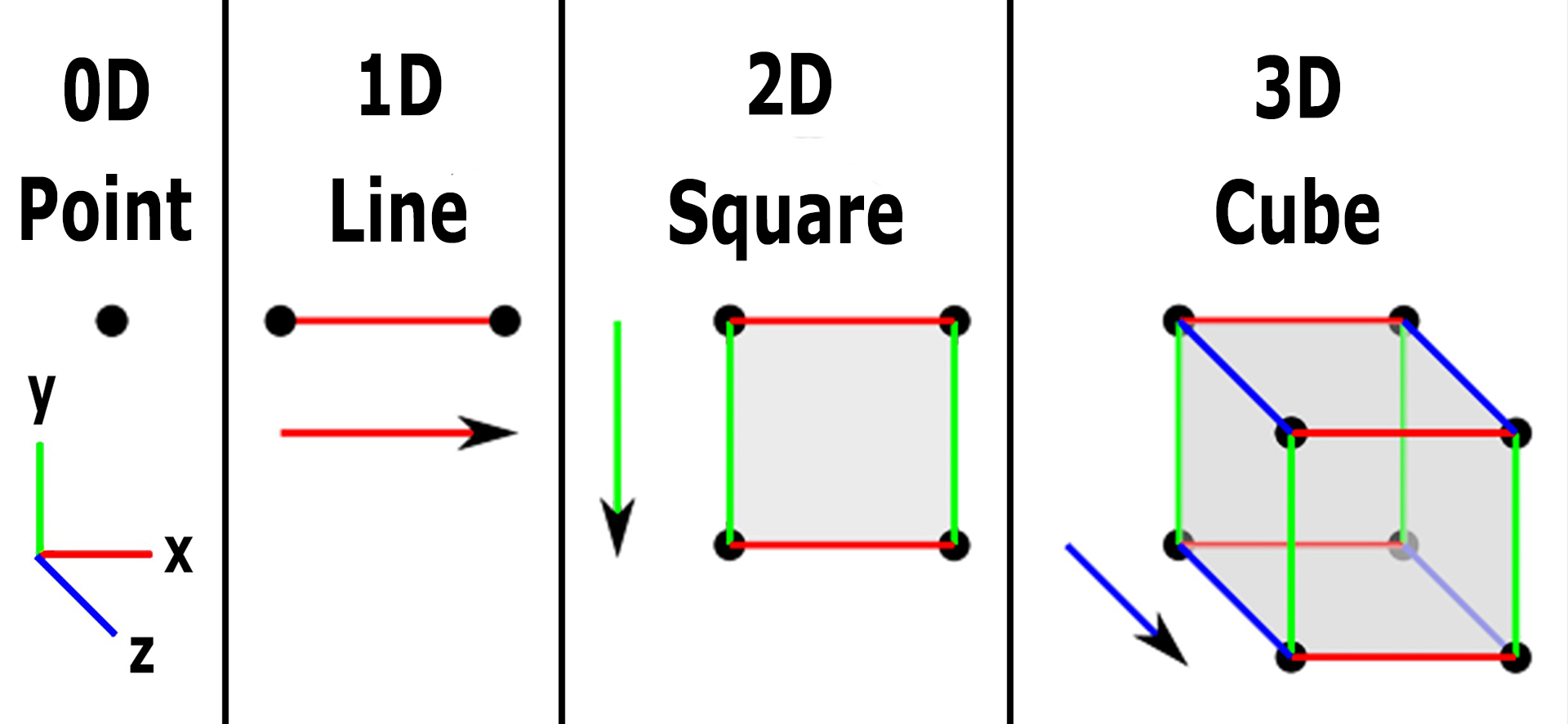
Our daily lives are so rooted in three dimensions. We build structures with height, objects have a certain width, and we travel distances with length. But mathematics isn’t confined to three. Equations smoothly extend to any number of dimensions, painting a picture of spaces far beyond what we can immediately sense. Trying to visualize these higher dimensions, though, is quite the puzzle. How do you even begin to imagine something that exists in a direction you can’t point to? It’s like trying to taste the color blue or hear the idea of fairness — our senses and natural understanding just aren’t built for it.

One helpful way to wrap our heads around this is through comparison. Consider a two-dimensional world, a flat surface inhabited by flat shapes. A circle in this world would appear as a simple line segment to a one-dimensional creature living on a line. Similarly, a three-dimensional sphere passing through this 2D plane would appear as a circle that grows bigger, reaches its maximum size, and then shrinks back to nothing. This comparison offers a key insight: a four-dimensional object moving through our 3D space might appear to us as a three-dimensional object that changes in unexpected and seemingly bizarre ways, perhaps shifting and transforming without any obvious external cause.

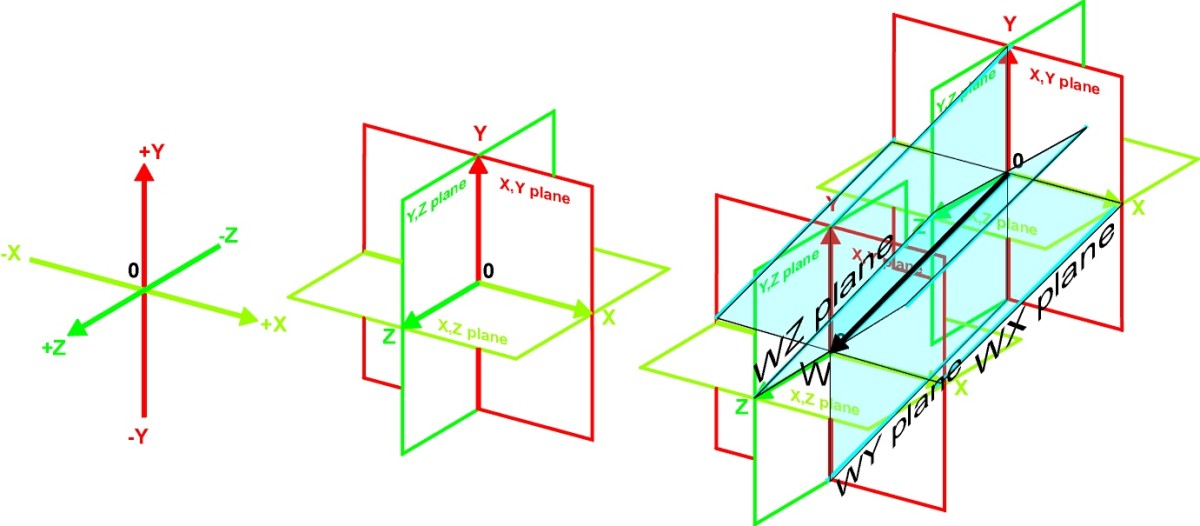
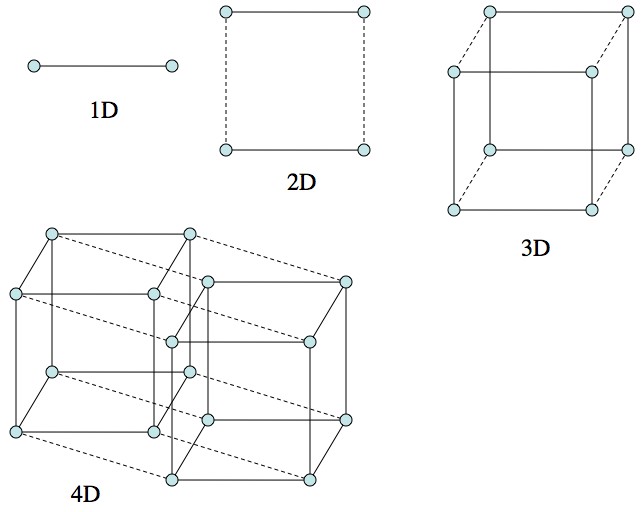
So, what might a four-dimensional object actually look like? It’s impossible to give a clear visual answer that our brains can fully process. However, we can use mathematical projections to get a sense of their complexity. Just as a three-dimensional cube can be shown on a two-dimensional surface as a square with lines connecting its corners (often looking like two squares nested inside each other), a four-dimensional hypercube, or tesseract, can be shown in our three-dimensional space. These projections appear as intricate arrangements of cubes within cubes, connected by lines, often looking like mind-bending puzzles that challenge our usual understanding of solid objects.

The Tesseract: A Glimpse of the Fourth Dimension’s Shadow

Showing Higher Dimensions in Our Everyday Reality

The tesseract acts as a key tool in our attempts to picture the fourth spatial dimension. Imagine taking a cube and then moving it in a fourth, right-angled direction for a distance equal to its side length. The “path” this movement takes in four-dimensional space creates the hypercube. Just as a cube has 8 corners, 12 edges, and 6 faces, a tesseract boasts 16 corners, 32 edges, 24 square faces, and 8 cubic cells. This step-by-step increase in elements shows the added complexity that comes with each new dimension.

When we show a tesseract in three dimensions, we get various interesting shapes. One common way it looks is like a cube inside another cube, with lines connecting their matching corners. Another way to show it can look like eight cubes arranged in a cross-like pattern. These images are just shadows of the true four-dimensional object, distorted by the process of “flattening” it into our space, much like a two-dimensional shadow of a three-dimensional cube doesn’t fully capture its cubic form. It’s like trying to understand a complex sculpture by only looking at its shadow on a wall — you get some idea, but the full picture remains hidden.

Understanding these images requires a shift in how we think. We need to move beyond our built-in three-dimensional intuition and embrace the mathematical rules that describe these higher-dimensional forms. While our visual part of the brain struggles to fully picture a tesseract, our mathematical understanding allows us to analyze its properties, its symmetries, and how it relates to simpler, lower-dimensional objects. It’s a testament to the power of abstract thought to venture beyond the limitations of what we can directly see.

The idea of a tesseract, while it might seem very abstract, has even popped up in popular culture, often used as a symbol of higher realities or advanced technology. This fascination highlights our human curiosity about what lies beyond what we can immediately perceive. While we may never truly “see” a tesseract in the same way we see a cube, the mathematical and conceptual exploration of such objects continues to push the boundaries of our understanding of space and dimensionality.

Life in Four Dimensions: What If We Lived There?

Considering the Possibilities of an Extra Way to Move

If we were inhabitants of a four-dimensional world, our experience of reality would be drastically different. Imagine being able to see all sides of a three-dimensional object at the same time without needing to move around it. A closed box would no longer be a barrier; we could simply “step around” its sides in the fourth dimension. This ability would fundamentally change our understanding of privacy, containment, and even what objects themselves are like.

Simple actions like tying a knot would become much more involved, perhaps even allowing for knots that are impossible to untie in three dimensions. Similarly, the way light and gravity behave could be very different in a four-dimensional space, potentially leading to entirely new physical laws. Our biological forms would also likely be very different, perhaps with circulatory and nervous systems that are far more intricate and efficient because of the added way to move. Think about how much easier it would be to connect different parts of a complex system without things getting tangled!

The very idea of “distance” would also take on a new meaning. Two points that seem far apart in our three-dimensional view could be incredibly close in the fourth dimension, connected by a “shortcut” that we can’t perceive. This idea is similar to concepts in theoretical physics, such as wormholes, which are often described as tunnels through higher dimensions that connect distant points in spacetime. While these are still just theories, the mathematical possibility hints at the profound implications of extra spatial dimensions.

However, such a world would also bring its own set of challenges. Navigating and interacting with a four-dimensional environment would require a completely new set of spatial reasoning skills. Our current three-dimensional brains, shaped by countless years of evolution in a 3D world, would likely struggle to grasp the complexities of movement and orientation in four dimensions. It’s a humbling thought to consider how limited our perception might be and how much more there could be to the universe than what our three-dimensional senses tell us.

Mathematical Tools for Higher Dimensions

Exploring the Abstract Language of Many Dimensions

While directly seeing higher dimensions remains out of reach, mathematics provides a powerful set of tools for exploring them. Concepts like vectors, matrices, and tensors can be easily extended to any number of dimensions, allowing us to describe and analyze multidimensional spaces with precision. The Pythagorean theorem, for example, extends beautifully to $n$ dimensions: the square of the distance between two points is the sum of the squares of the differences of their coordinates along each of the $n$ axes: $d^2 = (x_1 – y_1)^2 + (x_2 – y_2)^2 + \dots + (x_n – y_n)^2$.

Linear algebra gives us the framework for understanding transformations in higher dimensions, such as rotations and projections. Calculus extends to functions with multiple variables, allowing us to analyze rates of change and find the best solutions in these complex spaces. These mathematical tools aren’t just abstract ideas; they are fundamental to many areas of modern physics, including string theory, which suggests that the basic building blocks of the universe aren’t point-like particles but tiny vibrating strings existing in up to ten spatial dimensions (and one time dimension!).

The elegance and consistency of these mathematical frameworks offer strong support for the potential reality of higher dimensions, even if we can’t directly observe them. Just as the mathematical prediction of Neptune’s existence before it was seen through a telescope highlighted the power of theoretical reasoning, the mathematical consistency of higher-dimensional theories suggests that they might hold deeper truths about the nature of reality. It’s a reminder that our physical intuition, shaped by our limited experience, may not always be the best guide to the fundamental workings of the universe.

Exploring the mathematics of higher dimensions is like learning a new language — it takes effort and dedication, but it opens up a whole new way of understanding the world, or perhaps, worlds beyond our own. While we may never fully grasp what four spatial dimensions “look like” in a way that feels natural to us, the mathematical journey allows us to explore their properties, their implications, and their potential role in the grand scheme of the cosmos. It’s a testament to the human intellect’s ability to go beyond the limitations of our senses and delve into the realm of the abstract.

The Quest for Extra Dimensions: Why It’s Important

Unlocking the Secrets of the Universe

The question of whether extra spatial dimensions exist isn’t just a thought experiment; it has significant implications for how we understand the universe. Many unsolved puzzles in physics, such as why gravity is so much weaker than other fundamental forces and the nature of dark matter and dark energy, might find explanations in theories involving extra dimensions. For instance, some theories propose that gravity might be a strong force that “leaks” into our three-dimensional space from a higher-dimensional realm, thus appearing weak to us.

String theory, as mentioned earlier, needs extra dimensions to be mathematically consistent. While still a theoretical framework waiting for experimental confirmation, it offers a potential unified description of all fundamental forces and particles. The idea that these extra dimensions are “compactified” — meaning they are curled up into incredibly small sizes, making them impossible for us to directly see — is a key part of these theories. Imagine a garden hose: from far away, it looks one-dimensional, but up close, you can see its circular cross-section, a second, curled-up dimension.

Experiments at particle accelerators, like the Large Hadron Collider, are indirectly searching for evidence of extra dimensions by looking for unusual patterns in particle interactions that might suggest the influence of higher-dimensional physics. The detection of tiny black holes or the unexpected loss of energy and momentum could potentially indicate particles or forces escaping into extra dimensions. While no definitive proof has been found yet, the search continues.

Ultimately, the pursuit of understanding the nature of dimensionality is a pursuit of understanding the fundamental structure of reality. Whether four spatial dimensions are just a mathematical curiosity or a hidden aspect of our universe remains an open question. However, the theoretical exploration of these concepts continues to inspire new avenues of research and pushes the boundaries of human knowledge. It reminds us that the universe may hold wonders far stranger and more complex than we can currently imagine, waiting to be revealed through the combined power of mathematics, physics, and human curiosity. And who knows, maybe one day, we’ll find a way to catch a glimpse of that elusive fourth spatial dimension.

FAQ: Exploring the Realm of Dimensions

Answers to Your Intriguing Questions About Higher Spaces

Q: If we can’t see four spatial dimensions, how do scientists even talk about them?

A: That’s a really good point! While our brains aren’t designed to directly picture four spatial dimensions, we can use the powerful language of mathematics to describe them. Just like we can understand the concept of a black hole even though we can’t directly see its singularity, we can use equations and abstract reasoning to explore the properties and implications of higher-dimensional spaces. We also use comparisons with simpler, lower dimensions to build our understanding. Think of it like understanding how a shadow works to figure out the shape of the object casting it.

Q: Could there be even more than four spatial dimensions? What would those be like?

A: Absolutely! Mathematically, we can define spaces with any number of dimensions. Theories like string theory, as we discussed, propose the existence of up to ten spatial dimensions (plus one time dimension!). Picturing these even higher dimensions becomes increasingly difficult, but the mathematical rules remain consistent. Each additional dimension adds another way for movement and more complexity to the shape of space. Imagine the already mind-bending tesseract, and then try to picture moving it in yet another, completely new direction! It’s certainly a mental workout.

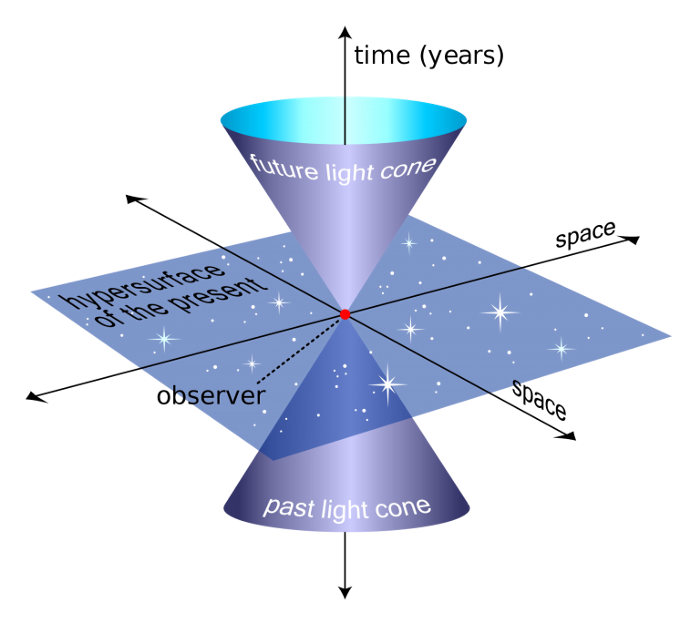
Q: Is the fourth dimension the same as time? I’ve heard that mentioned before.

A: That’s a common source of confusion! In Einstein’s theory of relativity, time is often referred to as the “fourth dimension” in the context of spacetime, a four-dimensional framework that combines our familiar three spatial dimensions with time. However, when we talk about “four spatial dimensions,” we specifically mean an additional dimension of space, at a right angle to length, width, and height, not time. While both are crucial for understanding the universe, they represent fundamentally different ideas. So, while spacetime is four-dimensional, the fourth dimension we’ve been exploring is purely about space.