Best Of The Best Info About Can Correlation Be Greater Than 1

Peering Beyond Perfect Alignment: The Curious Case of Correlation Exceeding Unity

Delving into Statistical Boundaries

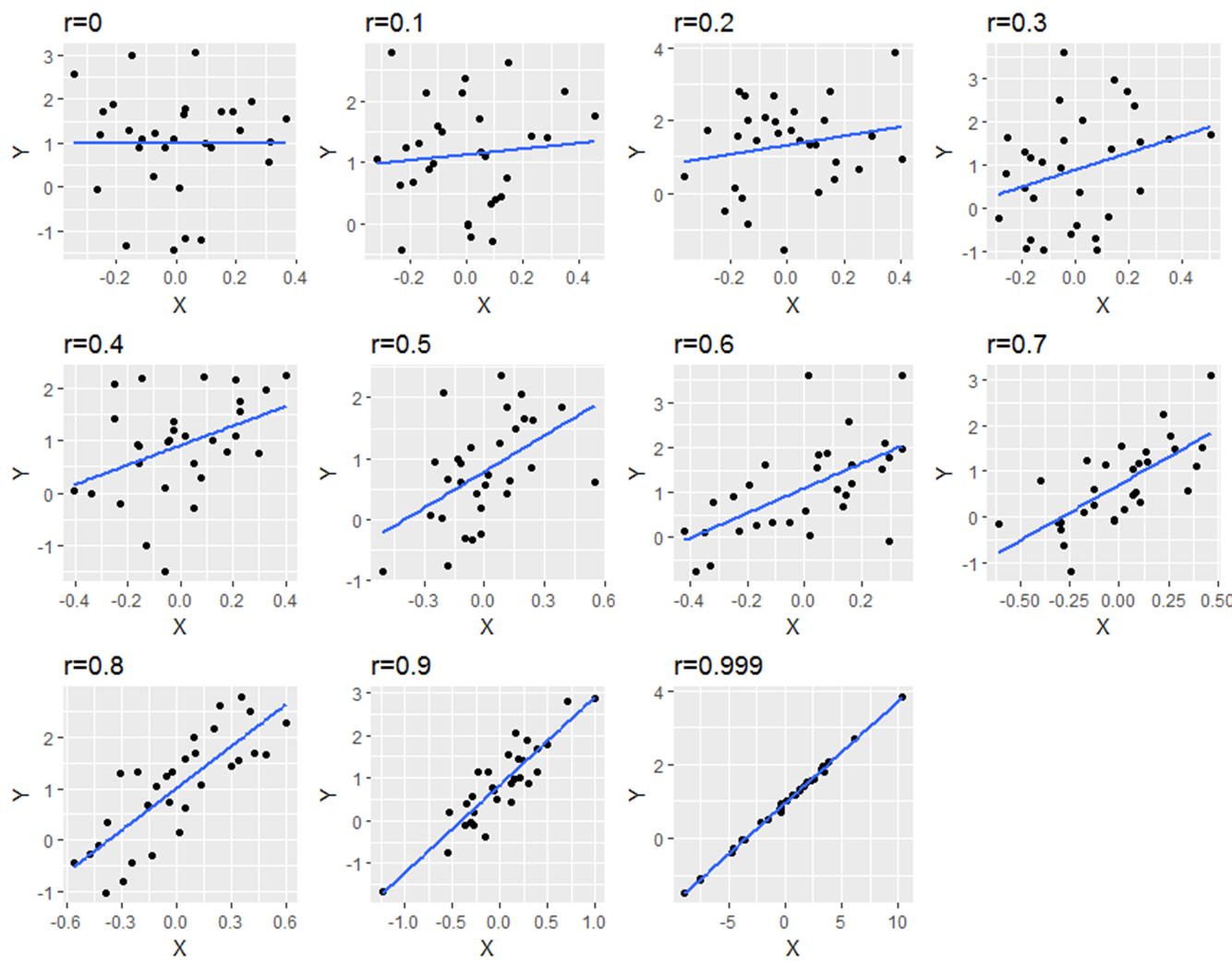
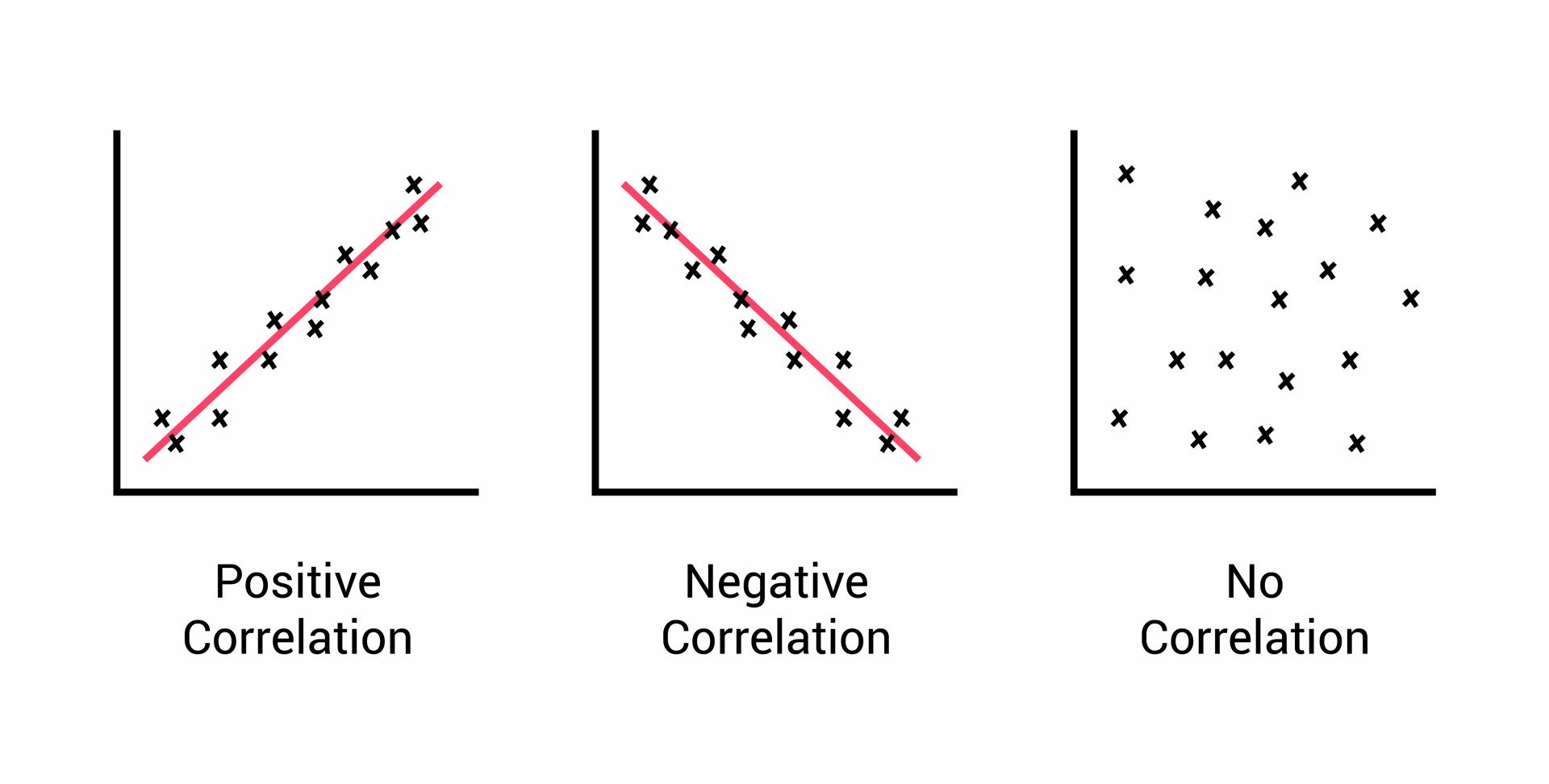
When we explore how two sets of numbers dance together, we often turn to correlation. It's a handy way to see if they tend to move in sync, in opposite directions, or just do their own thing. The Pearson correlation coefficient, that trusty 'r' we often see, neatly sums up this relationship on a scale from -1 to +1. A +1 score means they're perfect partners, always stepping in the same direction. A -1 suggests they're like opposite magnets, one goes up, the other goes down in perfect harmony. Zero? Well, that's like two people completely oblivious to each other's movements. But a thought might pop into your head: could this score ever break free from these limits, maybe even climb above a perfect 1? Let's have a closer look at this intriguing idea.

The way we mathematically calculate this correlation coefficient gives us a pretty firm "no" to that question. The formula itself, involving how much the numbers vary together compared to how much they vary on their own, inherently keeps the result within that -1 to +1 range. It's almost like trying to squeeze a foot-long ruler into an eleven-inch space — the physical constraints just won't allow it. The math behind correlation has its own built-in "container" that limits the possible outcomes.

However, the world of numbers isn't always so straightforward. While the standard Pearson correlation has these strict boundaries, the general idea of "correlation" or how things relate to each other can be looked at in different ways, especially when the relationship isn't a simple straight line. There are other statistical tools designed to measure these more complex connections. These alternative measures, while aiming to understand similar relationships, might not have the same -1 to +1 rulebook as Pearson's 'r'. Think of it as having different kinds of measuring tapes — some are rigid, some are flexible, and they might give you slightly different perspectives depending on what you're measuring.

So, while the definitive answer for the standard Pearson correlation is a solid "nope, can't go above 1," it's good to remember that how we understand connections between things can be broader than just this one measure. Different statistical tools offer different lenses through which we can examine these relationships. Knowing which tool we're using is key to understanding what its results actually mean and what limitations it might have. It's like understanding the rules of a game before you try to play it — each statistical measure has its own set of rules and boundaries.

Venturing Beyond Pearson's Reach: Other Ways to See Connections

A Broader View of How Things Link Up

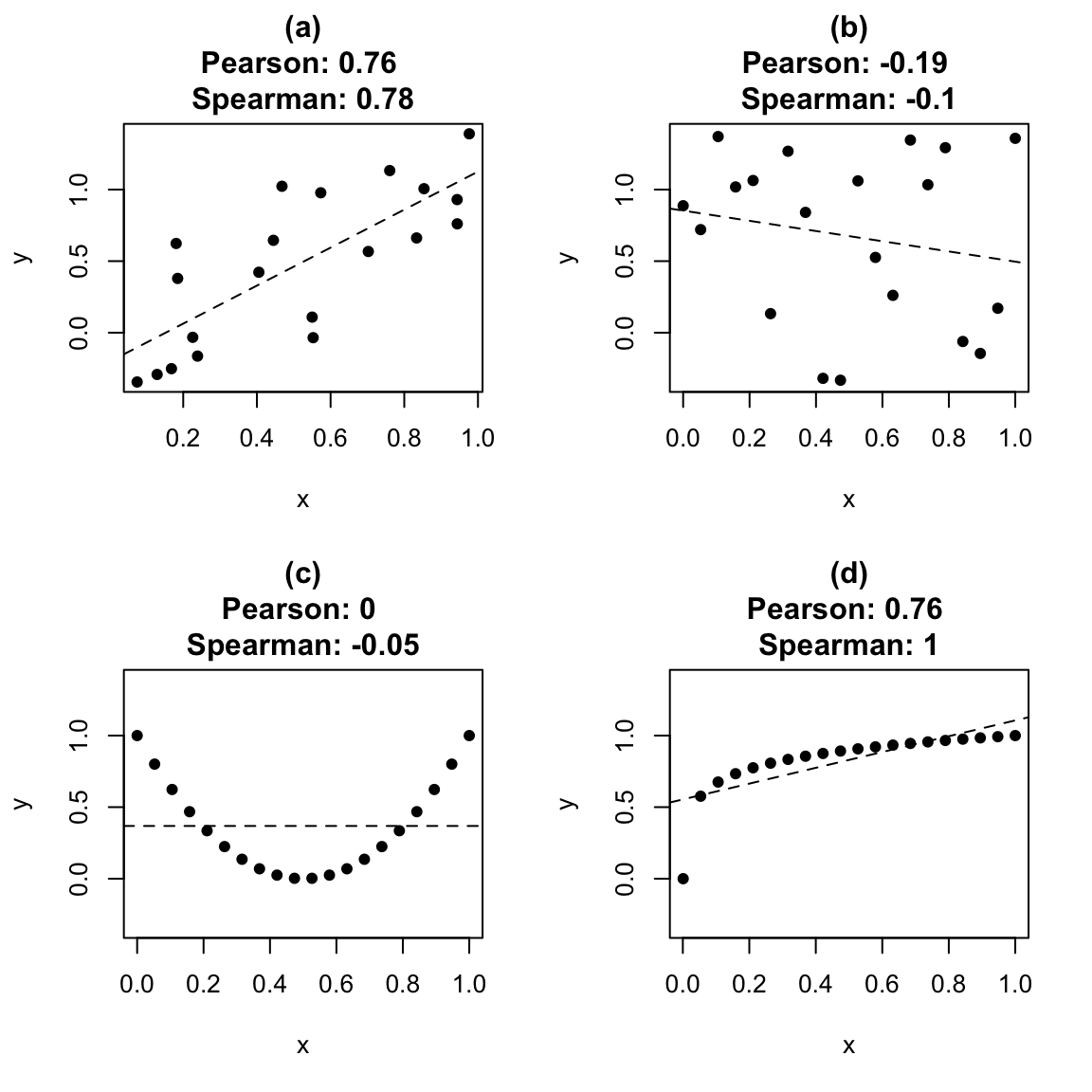
While the Pearson correlation is a workhorse in many basic statistical analyses, it's not the only way statisticians look at how variables connect. There's a whole toolbox of other methods designed to capture different kinds of relationships, especially when things don't follow a perfectly straight line or when we're dealing with different kinds of information. Take Spearman's rank correlation, for example. It looks at whether two sets of rankings tend to agree, even if the actual numbers themselves don't have a linear relationship. This can be really useful when you're dealing with things like customer satisfaction scores or rankings in a competition, where the order matters more than the precise difference between scores.

Then you have measures like mutual information, often used in information theory. This goes beyond just linear relationships and tries to quantify how much knowing one thing tells you about another. Its values don't have that strict -1 to +1 limit that Pearson's 'r' does. It's more about how much information the variables share, regardless of whether they move together in a straight line or in some more complicated pattern. Think of it as trying to understand how much two people's conversations overlap, even if they're talking about different subjects. There might still be shared information or context.

It's also worth mentioning that sometimes, in more advanced statistical modeling or theoretical discussions, you might see situations where transformations of data or specific ways of looking at things might produce values that seem to go beyond the usual correlation limits. However, these are often a result of the mathematical manipulations or how we're interpreting the transformed data, rather than a true case of the standard correlation breaking its own rules when applied to the original numbers. It's a bit like looking at a map projection — it can distort shapes and distances, but the underlying geography remains the same.

So, while the direct answer to whether a standard correlation can be bigger than 1 is still no, exploring these other ways of measuring association gives us a richer understanding of how variables can be connected. It reminds us that Pearson's correlation is a specific tool for a specific type of relationship, and the world of statistics offers many other ways to analyze the often intricate ways things relate to each other. It's about choosing the right tool for the specific job at hand and understanding the nuances of what each measure can tell us.

Common Misunderstandings and Potential Traps

Navigating the Twisty Paths of Statistics

The idea of correlation, while seemingly straightforward, can sometimes lead to confusion and even the mistaken belief that it can exceed its usual boundaries. One frequent pitfall is mixing up correlation with causation. Just because two things tend to move together doesn't automatically mean that one is causing the other. This is a really important point in statistics: correlation doesn't equal causation. Imagine finding that ice cream sales and the number of mosquito bites both go up in the summer. While they might be correlated, it's highly unlikely that buying ice cream attracts mosquitoes. A more probable explanation is a third factor, like warmer weather, that influences both. Jumping to conclusions about cause and effect based solely on correlation can lead to wrong understandings and bad decisions.

Another area where misunderstandings can arise is when we look at group data versus individual data. Correlations calculated for entire groups might not hold true for individuals within those groups. This is known as the ecological fallacy. For example, a study might show that countries with higher average internet access also have higher average life expectancy. However, this doesn't necessarily mean that individuals with more internet access within those countries live longer. There could be other factors at play at the individual level that are hidden when we look at averages. It's crucial to be aware of the level of analysis when interpreting correlation scores.

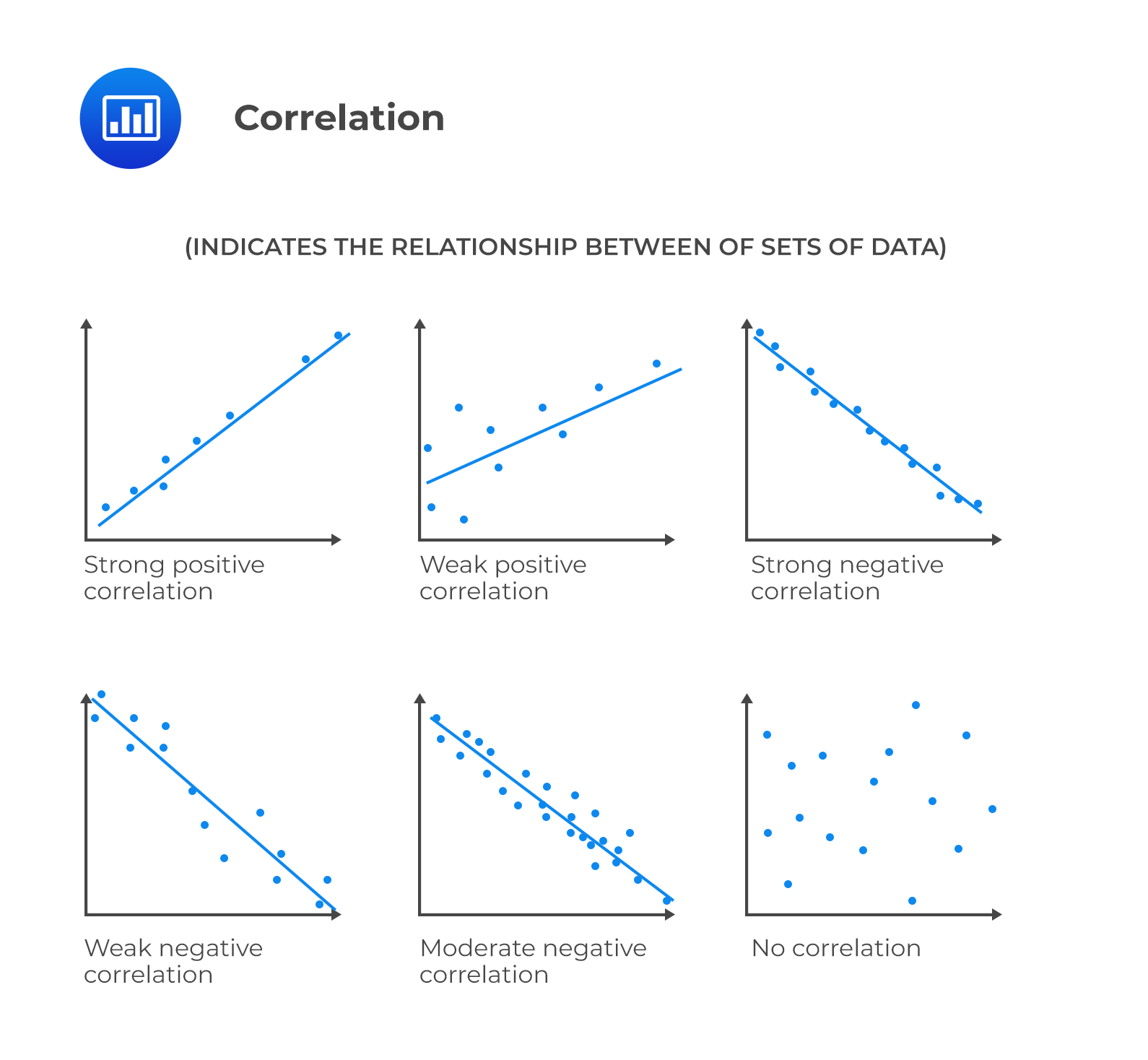
Furthermore, the quality of the data itself can play a big role in the calculated correlation. Outliers, those unusual data points that lie far away from the rest, can sometimes heavily influence the correlation, giving a misleading picture of the overall relationship. Also, if the relationship between two variables isn't a straight line but a curve, the Pearson correlation, which is designed to measure linear relationships, might be close to zero even if there's a strong, consistent pattern. It's always a good idea to look at your data visually, perhaps with a scatter plot, to spot any outliers or non-linear patterns that might affect how you interpret the correlation. Think of it as looking at the ingredients before you bake a cake — bad ingredients can lead to a bad outcome.

Finally, be cautious of what are called spurious correlations — relationships that appear statistically significant but have no real underlying connection. With a large enough dataset and enough variables, it's statistically probable that you'll find some pairs that show a high correlation just by random chance. This is where critical thinking and knowledge of the subject matter are essential to distinguish meaningful relationships from coincidental ones. Just because two lines on a graph happen to move in a similar way doesn't mean they're actually related. It's like finding two people in a big city who happen to be wearing the same color shoes on the same day — it's probably just a coincidence.

The Significance of Context and Wise Interpretation

Looking Beyond the Raw Number

While the numerical value of a correlation coefficient gives us a measure of how linearly related two variables are, what that number actually means depends a lot on the context of the data and what question we're trying to answer. A correlation of 0.7 might be considered quite strong in some fields, like social sciences where human behavior introduces a lot of complexity, but might be seen as relatively weak in others, such as physics where relationships are often more precise and predictable. There's no magic number that universally defines a "strong" or "weak" correlation; it really depends on what's typical in that particular area of study. Think of it like the temperature of a room — what feels "warm" depends on whether you're used to living in the Arctic or the tropics.

Additionally, when we interpret correlation scores, we need to consider the size of our sample. A high correlation based on only a few data points might not be statistically reliable or applicable to a larger group. Statistical tests for significance help us determine how likely it is that the correlation we observed is just due to random chance. A larger sample size gives us more confidence in our findings, even if the correlation coefficient isn't extremely high. It's like taking a poll — a poll with more respondents is generally more representative of the overall population.

It's important to remember that correlation only tells us about the linear relationship between two variables. If the relationship is curved, the Pearson correlation might be close to zero even if there's a strong association. Always consider looking at your data visually with scatter plots to get a sense of the underlying pattern. A curved relationship won't be well-captured by a linear measure. It's like trying to measure the distance around a circular track by only walking in straight lines — you'll underestimate the total distance.

Ultimately, understanding a correlation coefficient involves more than just looking at the number. It requires a good grasp of the data, the context of the research, and the limitations of the specific correlation measure used. Always think about potential other factors, the possibility of non-linear relationships, and whether your findings are statistically meaningful. A well-understood correlation can offer valuable insights, but a poorly interpreted one can lead to incorrect conclusions. It's about understanding the story the numbers are trying to tell, not just the numbers themselves.

Common Questions About Correlation

Your Inquiries Addressed

Q: Can a correlation coefficient ever reach, say, 1.2?
A: Definitely not! The standard Pearson correlation coefficient is designed to live within the boundaries of -1 and +1. A value like 1.2 is statistically out of bounds under normal circumstances. If you ever encounter such a number, it's a red flag to double-check your calculations or the source of the information — something has likely gone wrong. It's similar to saying you have a probability of 120% — it doesn't fit within the standard rules.

Q: What does it mean if I get a correlation of 0?
A: A correlation of 0 suggests that there's no linear relationship between the two variables you're looking at. However, this doesn't automatically mean there's no relationship at all. There could still be a non-linear connection. It's always a good idea to visualize your data to see if there are any underlying patterns that a linear correlation wouldn't pick up. Think of it like two people walking in a park — they might not be walking directly towards or away from each other, but their paths could still cross or run parallel at certain points.

Q: Is a really high correlation always a good sign?
A: Not necessarily. While a high correlation can indicate a strong linear link, it doesn't tell you anything about whether one variable is causing the other. Moreover, in some statistical models, a very high correlation between the predictor variables (this is called multicollinearity) can actually cause problems with the model's stability and how easy it is to interpret the results. It really depends on the context and what you're trying to achieve with your analysis. Sometimes, a moderate correlation can be more informative than an extremely high one. It's like having too many cooks in the kitchen — it can sometimes lead to confusion rather than a better outcome.